Graphical Method of Linear Programming Problem
Example 1: Use
the graphical method to solve the following LP problem.
Maximize Z = - X1 + 2X2
Subject to the constraints
- X1
+ 3X2 £
10
X1 + X2
£ 6
X1
- X2
£ 2
and X1 , X2 ≥ 0
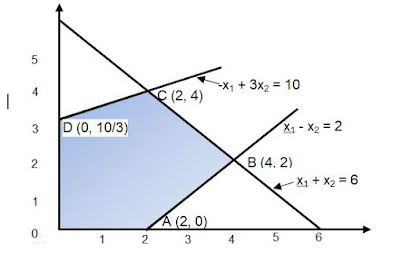
Solution: In this problem there are three constraints. Thus the feasible region will be bounded by three lines on X and Y axes. Changing the constraints into equalities and putting X1 =0 and then X2 = 0 alternately, we can get the co-ordinates of two points corresponding to each line i.e.
Point I Point II
-X1 + 3X2 = 10 X1 = 0, X2
= 10/3 X1 = -10, X2
= 0
X1
+ X2 = 6 X1 = 0, X2 =
6 X1 = 6, X2
= 0
X1 - X2 = 2 X1 = 0, X2 = -2 X1 = 2, X2 = 0
The coordinates of extreme points of the feasible region
are:
O = (0, 0), A = (2, 0) B = (4, 2), C = (2, 4), D = (0, 10/3)
These values are illustrated in figure mentioned below:
The value of the objective function at each of these extreme
points is as follows:
|
Extreme point |
Coordinates (X1, X2) |
Objective function value Z= -X1 + 2X2 |
|
O A B C D |
(0, 0) (2, 0) (4, 2) (2, 4) (0, 10/3) |
-1(0) + 2(0) =
0 -1(2) + 2(0) = -2 -1(4) + 2(2) = 0 -1(2) + 2(4) = 6 -1(0) + 2(10/3) = 20/3 |

टिप्पणियाँ
एक टिप्पणी भेजें